1. 引言
在过去的十年中,神经网络对图像分类、目标检测、目标跟踪,实例分割等任务推理的准确性有了显著提高,这通常是通过高度过度参数化的模型实现的。但是会出现以下疑问:网络的深度的持续增加是否也能同步提高分类任务的准确率?复杂的结构和巨大的参数量是否也能提高神经网络的表征性能?基于以上问题,卷积神经网络经历了结构愈发复杂,参数愈发繁多的发展阶段,VGG网络层数在短时间内发展到了惊人的16到19层,更有甚者研究出了高达22层的GoogleNet。
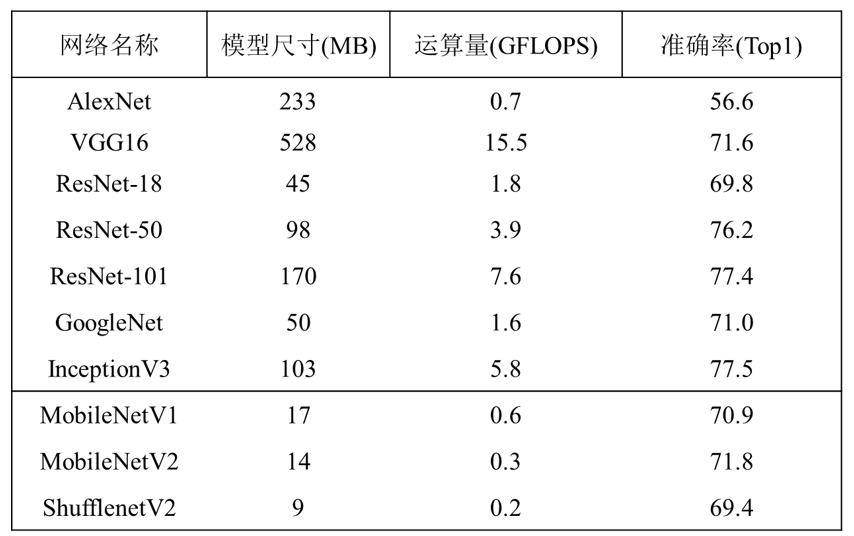
然而,神经网络的优异性能是以高昂的计算复杂度和巨大的内存消耗作为代价的,上表 中的上半部分列举了部分常用网络的模型尺寸,和推理一张标准 224 × 224 大小的 RGB图片的运算量和准确率。从表中可以看出:随着网络的发展,其规模逐渐扩大,网络的参数量越来越多,运算量也越来越大。这会导致难以将其部署在某些资源受限的设备中,极大地限制了神经网络的应用场景。例如在物联网(Internet of Things,IoT)等场景中,嵌入式系统不仅缺乏丰富的运算和存储资源,同时对低功耗也有着十分迫切的需求。-
此外,自动驾驶等应用对网络推理的实时性要求极高,否则会存在安全隐患。因此,各式各样的深度神经网络压缩和加速技术应运而生,在保证网络准确率的同时试图去除网络中的冗余,即在网络性能以及运算代价之间寻找良好的权衡。-
因此,迫切需要优化模型的技术,以减少模型尺寸、实现更低的功耗和更快的推理速度。深度学习领域对这些问题从事了大量的研究,主要有两个方面:
- 设计更加高效的网络架构,用相对较小的模型尺寸达到可以接受的精确度,例如上表中的 MobileNetV1、MobileNetV2 和 ShufflenetNetV2。
- 通过压缩、编码等方式减小网络规模。量化是工业界广泛采用的压缩方法之一。-
通常情况下,可以共同使用以上两种策略来取得令人瞩目的成果。例如,TensorFlow 量化的MobileNetV1 仅为 4.8MB,这甚至比大多数 GIF 动图还要小,从而可以轻松地部署在任何移动平台上。
2. 硬件背景
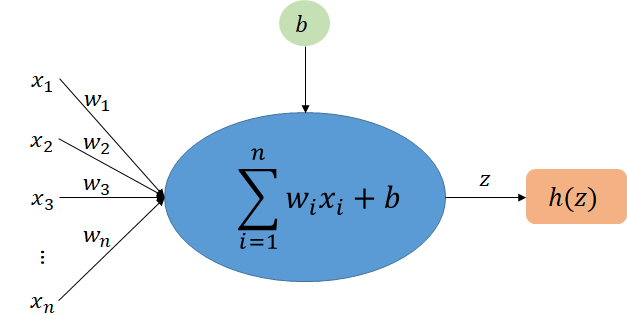
在深入研究技术细节之前,我们首先来了解神经网络量化的硬件背景以及它如何在设备上实现高效推理。神经网络是使用计算机模拟生物神经系统中人类思维方式的算法,它的基本单位是人工神经元,通过相互连接形成一张神经网络。下图展示了单个神经元的计算结构:
- x1,x2,…,xnx_1,x_2,…,x_nx1,x2,…,xn表示输入;
- w1,w2,…,wnw_1,w_2,…,w_nw1,w2,…,wn表示权重参数;
- bbb表示偏置项。
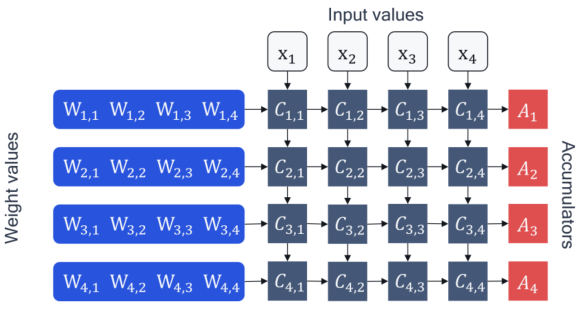
在神经网络的计算图中,将每个神经元的计算合并为∑i=1nwixi+b\sum_{i=1}^n w_ix_i+b∑i=1nwixi+b形式的加权求和,通过非线性激活后得到该节点的输出,这个输出也可以作为下一个神经元的输入。由此可见,神经网络算法的基础运算是矩阵的乘法,那么硬件计算单元就应该通过并行执行尽可能多的计算来提高神经网络推理的效率,下图为硬件加速器中单个神经元计算矩阵乘法y=Wx+by=Wx+by=Wx+b的示意图:
该神经网络加速器包含两个基本部件处理元件Cn,mC_{n,m}Cn,m和累加器AnA_nAn。计算过程中首先用偏置值bnb_nbn加载累加器,然后将权重Wn,mW_{n,m}Wn,m和输入xm\mathbf{x}_mxm加载到数组中,并在相应处理元件Cn,m=Wn,mxmC_{n,m}=W_{n,m}\mathbf{x}_mCn,m=Wn,mxm计算它们的乘积,最后将结果添加至累加器AnA_nAn:
An=bn+∑mCn,mA_n=b_n+\sum_{m}C_{n,m}An=bn+m∑Cn,m
上述操作也被称为乘法累加(Multiply-Accumulate,MAC)。对于较大型的矩阵向量乘法,硬件层面进行的操作是:
- 重复进行多次MAC操作,一旦循环运算完成,累加器中的数据值将被移动回存储器,用于下一个神经网络层;
- 神经网络通常使用FP32类型权重参数和激活进行训练,如果基于FP32执行推理,处理元件和累加器将必须支持浮点逻辑,并且需要将32位数据从内存传输到处理单元;
- MAC操作和数据传输消耗了神经网络推理期间消耗的大量能量。因此,通过使用这些量的低位定点或量化表示,可以获得明显的益处。低位定点表示,如INT8,不仅减少了数据传输量,而且还减少了MAC操作的大小和能耗。-
相对于浮点数运算,整数的加法器的硬件结构要简单得多,这也在一定程度上降低了功耗。这是因为浮点数的加减法不是简简单单地将尾数加在一起,要考虑阶码。浮点数加减法的实现方法就是以绝对值大的数字为基准,移动绝对值小的数字,然后做加减。所以硬件模块首先要通过比较大小来选择减数和被减数,选择阶码和符号,然后进行移位尾数相加。
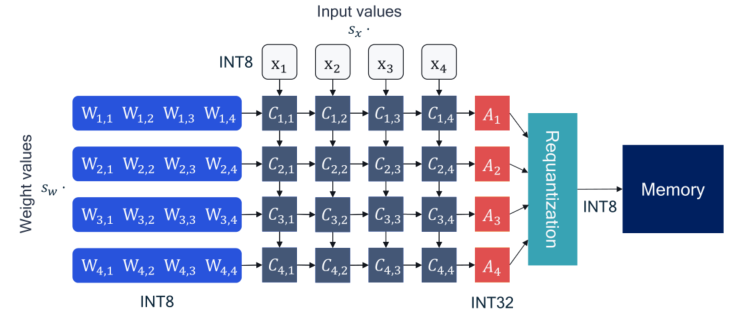
为了从浮点运算转移到高效的定点运算,需要一种将浮点向量转换为整数的方案,也就是量化操作。为了防止溢出,累加器仍然是采用浮点计算,所以一般不会考虑偏置值bnb_nbn的量化。上图为引入量化操作后神经网络加速器的变化,量化后的运算可以表示为:
A^n=∑mW^n,mx^m=∑m(swWn,mint)(sxxm)\hat{A}_n =\sum_m \hat{W}_{n,m} \hat{\mathbf{x}}_m =\sum_m (s_wW_{n,m}^{int} ) ({s_x\mathbf{x}}_m)A^n=m∑W^n,mx^m=m∑(swWn,mint)(sxxm)
其中sw,sxs_w,s_xsw,sx分别表示权重和输入的浮点转换因子,示例中对权重和激活使用了INT8的量化,存储在32位累加器中的数值需要写入内存,然后才能由下一层使用。为了减少数据传输和下一层神经元操作的复杂性,这些数值被重新量化回INT8类型。-
量化以低于浮点精度的位宽计算和存储张量,量化模型以降低的精度而不是全精度(浮点)值对张量执行部分或全部操作,使得模型的表示更加紧凑,从而可以在许多硬件平台上进行高性能矢量化运算。在神经网络量化过程中,权重和激活通常被保存为低bit精度而不是训练时的FP16或者FP32。工业界通常选择 INT8 量化,从FP32到INT8,可以在以下几点实现性能提升:
- 模型存储缩小4倍;
- 内存带宽减少2-4倍;
- 由于内存带宽的节省和 INT8 算法的计算速度加快,推理速度提高了 2-4 倍(确切的加速速度因硬件、runtime和模型而异)。
3. 量化基本概念
3.1 浮点量化
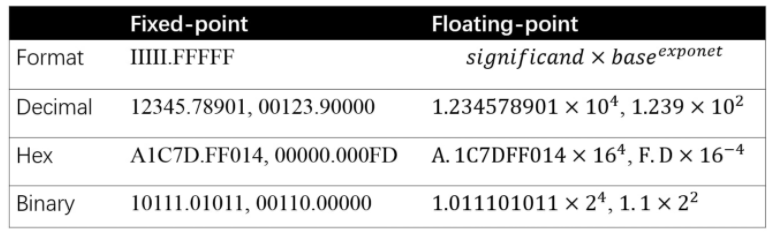
由于量化桥接了固定点(fixed point)和浮点(floating point),在接触相关研究和解决方案之前,有必要先了解它们的基础知识。定点和浮点都是数值的表示,它们的区别在于:将整数(integer)部分和小数(fractional)部分分开的点以及点在哪里。定点保留特定位数整数和小数,而浮点保留特定位数的有效数字(significand)和指数(exponent)。
上图中给出了定点和浮点表示的格式和示例。对于定点,I 表示整数,F 表示 IIIII.FFFFF 中小数部分。对于浮点数,base =2、10、16分别对应二进制、十进制和十六进制。-
在指令集(Instruction Set Architecture)的内置数据类型中,定点是整数,浮点是二进制格式。一般来说,指令集层面的定点是连续的,因为它是整数,且两个邻近的可表示数字的间隙是 1 。另一方面,浮点代表实数,其数值间隙由指数确定,因而具有非常宽的值域。-
FP32的单精度值具有 4 个字节,包括一个符号位、一个 8 位 二进制指数和一个 23 位尾数,所以32 位数值最大整数是232−12^{32}-1232−1,浮点值域为 [(2−223)×2127,(223−2)×2127][(2-2^{23})\times2^{127},(2^{23}-2)\times2^{127} ][(2−223)×2127,(223−2)×2127],值越接近零就越准确。在给定指数时,浮点在不同范围内拥有数值数量相同。因此,将网络从FP32转换为INT8并不像数据类型转换截断那样简单。
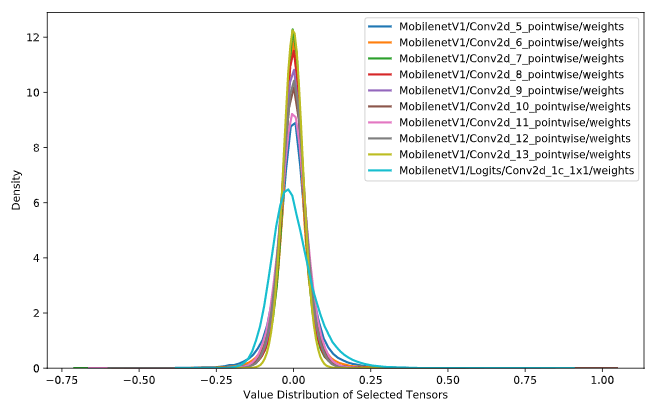
幸运的是,神经网络权重的值分布范围很有限,非常接近于零。上图中给出了 MobileNetV1 中10层(拥有最多值的层)的权重分布。该值范围为(−1,1),量化浮点是使用像xfloat=xscale×xquantizedx_{float}=x_{scale}\times x_{quantized}xfloat=xscale×xquantized的方法将FP32映射到INT8,这里xfloatx_{float}xfloat表示FP32,xquantizedx_{quantized}xquantized表示量化的INT8权重,xscalex_{scale}xscale是量化比例因子。
3.2 均匀量化与非均匀量化
量化操作是用一组离散符号或者整数值来近似连续信号的过程,最简单直接的方法就是将连续值通过仿射变换线性地映射到距离最近的整型值上。浮点数在经过缩放,取整,偏移和溢出保护等操作后即可得到量化后在离散空间的结果,该方法一般被称为线性量化或均匀量化。由于其易于实现,因而应用最为广泛。均匀量化至n比特数时,如果使用无符号整型数,其量化值的范围是{0,…,2n−1}\{0,…,2^{n}-1\}{0,…,2n−1};如果使用有符号整型数,其量化值的范围是{−2n−1,2n−1−1}\{-2^{n-1},2^{n-1}-1\}{−2n−1,2n−1−1}内的整数,如下图左边所示(黄色点即为量化后的定点值)。
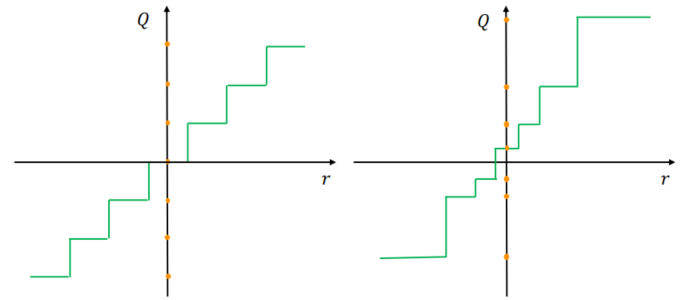
均匀量化的操作如下所示:
xfloat=xscale×(xquantized−xzero_point)x_{float}=x_{scale}\times (x_{quantized}-x_{zero\_point})xfloat=xscale×(xquantized−xzero_point)
大多数情况下量化选用无符号整数,那么 INT8 值域为 [0,255] 。 零点偏移xzero_pointx_{zero\_point}xzero_point 在这种情况下更有意义,具体而言,如下面的等式所示,量化浮点值可以分为两个步骤:
xfloat∈[xfloatmin,xfloatmax]x_{float} \in [x_{float}^{min},x_{float}^{max}]xfloat∈[xfloatmin,xfloatmax]xscale=xfloatmax−xfloatminxquantizedmax−xquantizedminx_{scale}=\frac {x_{float}^{max}-x_{float}^{min}}{x_{quantized}^{max}-x_{quantized}^{min}}xscale=xquantizedmax−xquantizedminxfloatmax−xfloatminxzero_point=xquantizedmax−xfloatmax/xscalex_{zero\_point}={x_{quantized}^{max}-x_{float}^{max}}/x_{scale}xzero_point=xquantizedmax−xfloatmax/xscalexquantized=xfloat/xscale+xscalex_{quantized}=x_{float}/x_{scale}+x_{scale}xquantized=xfloat/xscale+xscale
- 通过在权重张量(FP32)中找到 min 和 max 值从而确定xscalex_{scale}xscale 和 xzero_pointx_{zero\_point}xzero_point 。
- 将权重张量的每个值从 FP32 转换为 INT8 。-
注意:当浮点运算结果不等于整数时,需要额外的舍入步骤。例如将 FP32 值域 [−1,1] 映射到 INT8 值域 [0,255],有xscalex_{scale}xscale=2/255,而xzero_pointx_{zero\_point}xzero_point=255-255/2约等于127。
均匀量化可以用以下公式表示:
xint=clamp(round(xfscale+zero_point),−2n−1,2n−1−1)x_{int}=clamp(round(\frac{x_{f}}{scale}+zero\_point),-2^{n-1},2^{n-1}-1)xint=clamp(round(scalexf+zero_point),−2n−1,2n−1−1)clamp(x,min,max)={ min, x≤minx,min≤x≤ max,max,x≥ maxclamp(x,min,max)=\begin{cases} min, x\leq min\\x,min\leq x \leq max, \\max,x\ge max \end{cases}clamp(x,min,max)=⎩⎨⎧ min, x≤minx,min≤x≤ max,max,x≥ max
其中:
- xfx_{f}xf为原浮点数,xintx_{int}xint为量化后的定点值
- scale是量化系数;
- zero_point为偏移量,表示浮点值0对应的量化定点值;
- round为取整函数;
- n为量化位宽,比如int8量化时n=8;
- clamp为钳位函数,将不断增加、减小或随机变化的数值限制在一定的范围内;
而非均匀量化则采用一些非线性函数,例如采用对数分布、k-means聚类等方式确定原浮点数与定点值之间的对应关系。虽然相较于均匀量化,非均匀量化能根据原数据分布特点采取合适的映射方式,能更好地保持精度,但很难被部署在硬件上。
3.3 对称量化与非对称量化
针对均匀量化,不同量化算法其研究核心都是如何确定量化比例系数scale和偏移量zero_point,尽可能地在保证模型压缩效果的同时减少量化误差的引入。其中,scale的计算公式如下所示:
scale=β−α2n−1scale=\frac{β-α}{2^n-1}scale=2n−1β−α
[α,β]为原浮点值的截取范围,n为量化位宽,scale决定了量化后的分区数量(共2n−12^n-12n−1个分区)。确定截取范围的过程也称为校准过程,最简单的方式就是直接取原数值的最大最小值,即α=xminα=x_{min}α=xmin、β=xmaxβ=x_{max}β=xmax,通常这是一种非对称的量化方式,因为α≠β,下图为非对称量化的示意图:
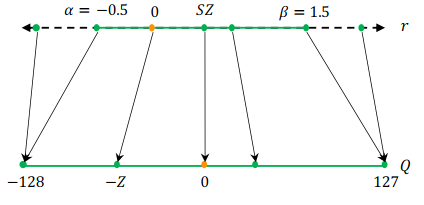
由于非对称量化需要加入零点偏移值zero_point(因为0往往有着特殊的含义,如padding),会增加计算复杂度,通常大家会取值−α=β=max(∣xmin∣,∣xmax∣)-α=β=max(|x_{min}|,|x_{max}|)−α=β=max(∣xmin∣,∣xmax∣),也就成为了对称量化。
xint=round(xrscale)x_{int}=round(\frac{x_{r}}{scale})xint=round(scalexr)
还有一种处理方式是使量化后的区间[a,b]也不以零点为中心,且满足ab=αβ\frac{a}{b}=\frac{α}{β}ba=βα,那仍然是对称量化,不需要引入零点偏移值zero_point。
但是,当权重和激活值分布不均衡的时候(例如经过Relu后的激活值都为非负数),非对称量化可以得到更精准的裁切范围,避免有效信息被压缩甚至是被淹没。
这种直接采用min/max的方式容易受到激活值中异常数据的影响,导致截断范围变大,影响量化精度。为解决这个问题,通常使用percentile代替min/max,也就是使用特征图中第i个最大值/最小值来代替min/max,或采用使得浮点值和量化值之间kl散度最小的β和α。
3.4 PTQ和QAT
无论以上哪种方法,量化操作都对数据做了近似,丢失了部分高频信息,必然会引入量化误差。但由于神经网络本身具有一定的鲁棒性和容错性,少量的量化误差并不会影响网络性能,仅通过训练后量化(Post-training Quantization,PTQ)即可用于部署。但如果量化误差过大超过神经网络本身的韧性,其性能将会呈现一定地下降。此时,需要对网络参数进行重训练以适应量化操作带来的数据分布变化,该训练过程一般被称为量化感知训练(Quantization Aware Training,QAT)。
地平线芯片算法工具链支持PTQ和QAT两种量化方式,目前已经在社区开放了地平线社区QAT量化方案 。另外,地平线还支持将模型前后端的量化/反量化节点的计算融入模型的前后处理中,以减少数据重复遍历的时间消耗,相关内容可以参考反量化节点的融合实现。
3.4.1 PTQ
PTQ 是使用一批校准数据对训练好的模型进行校准,将训练过的FP32模型直接转换为定点计算的模型,过程中无需对原始模型进行任何训练。只对几个超参数调整就可完成量化过程, 且过程简单快速,无需训练,因此此方法已被广泛应用于大量的端侧和云侧部署场景。但是,由于PTQ的目的就是为了快速量化,因此大部分方法都集中优化单层网络的局部误差,而非考虑整体网络任务的损失。相关技术细节可以参考用户手册PTQ量化快速上手章节。
3.4.2 QAT
QAT 是将训练过的模型量化后又再进行重训练。在整个训练过程会保留一套全精度权值拷贝,在前向传播过程中,该全精度权值会被量化至目标整型数据精度,使用该量化权值计算网络输出以及损失函数。在权值更新时,则会将梯度的微小变化累积到全精度权值上,这样在经过多次更新后,权值才有可能会被量化至相邻的量化等级。在实际训练过程中,一般会使用伪量化,即所有的操作仍然可以使用全精度数进行计算,会将权值和激活值量化为离散值后再反量化回原本的范围。但是,由于它需要对模型进行训练, 对操作人员技术要求较高。相关技术细节可以参考用户手册QAT快速上手章节。
4. 地平线PTQ量化
地平线芯片算法工具链从芯片端侧部署优化的角度出发,量化方式默认为对称量化,非对称量化仅会在少数情况下会被default校准方式搜索到。-
PTQ是使用一批校准数据对训练好的模型进行校准,以获取量化阈值[α,β],然后使用由量化阈值计算而来的量化比例因子scale进行量化。假设量化位宽为n,scale的计算方式如下如下:
scale=β−α2n−1scale=\frac{β-α}{2^n-1}scale=2n−1β−α
量化阈值选择常见方法有:
1. Weight 量化-
针对weight的量化阈值大都默认选择一个卷积核对应一个量化阈值T的max方法,计算公式为:
T=max(abs(max),abs(min))T=max(abs(max),abs(min))T=max(abs(max),abs(min))
2. Featuremap量化-
针对featuremap量化,地平线的PTQ量化转换工具hb_mapper makertbin提供了多种校准方法,通过在yaml文件中配置calibration_type参数进行选择,主要有:
- max校准方法-
选择输入的featuremap的最大值vmax,最小值vmin的绝对值作为阈值,计算公式为:T=max(abs(vmax),abs(vmin))T=max(abs(vmax),abs(vmin))T=max(abs(vmax),abs(vmin))另外,还可以在yaml中配置max_percentile参数来调整max校准的截取点,常用配置选项有:0.99999/0.99995/0.99990/0.99950/0.99900。 - kl散度校准方法-
kl散度是用来计算量化后int数据的分布P和float的分布Q这两个分布的距离。通过遍历可能的截断范围,并根据每个截断范围进行量化,然后对比量化后的int数据分布和量化前float的数据分布,计算kl散度,找到kl散度最小的截断范围作为最终量化时使用的阈值。kl散度的计算公式如下:KL(P,Q)=∑i=1nPi(log2Pi−log2Qi)KL(P,Q)=\sum_{i=1}^n P_i(log_{2}{P_i}-log_{2}{Q_i})KL(P,Q)=i=1∑nPi(log2Pi−log2Qi) - mix校准方法-
mix 是一个集成多种校准方法的搜索策略, 能够自动确定量化敏感节点,并在节点粒度上从不同的校准方法中挑选出最佳方法,最终构建一个融合了多种校准方法优势的组合校准方式。详细过程如下:-
**Step1:**采用kl校准方法,计算当前模型中节点的量化敏感度(使用余弦相似度来衡量),将值小于特定阈值的节点定义为 量化敏感节点(对模型量化精度影响较大的节点)。-
**Step2:**遍历所有量化敏感节点,在每一个节点上尝试Max、Max-Percentile 0.99995和KL三种校准方法, 并为该节点选出最佳的校准方法,最终得到Mix校准模型。-
**Step3:**评估Mix、Max、Max-Percentile 0.99995和KL校准模型的累积误差情况,输出最优模型。 - default校准方法-
default是一个自动搜索的策略, 会尝试从系列校准量化参数中获得一个相对效果较好的组合。详细过程如下:-
**Step1:**尝试Max、Max-Percentile 0.99995和KL三种校准方法,计算得到分别的余弦相似度。 如果三种方法中的最高余弦相似度小于0.995,进入Step2;反之,返回最高相似度对应的阈值组合。-
**Step2:**尝试Max-Percentile 0.99995和perchannel量化的组合方法,如果四种方法中的最高余弦相似度小于0.995,进入Step3; 反之,返回最高相似度对应的阈值组合。-
**Step3:**选取Step2中最高余弦相似度对应的方法,应用非对称量化作为第5种方法,根据余弦相似度选取5种方案中的最佳方案, 返回对应的阈值组合。
参考文献
- Nagel M, Fournarakis M, Amjad R A, et al. A white paper on neural network quantization[J]. arXiv preprint arXiv:2106.08295, 2021.
- 李博闻. 深度神经网络量化及其硬件加速研究[D].浙江大学,2022.DOI:10.27461/d.cnki.gzjdx.2022.000973.