1.概述
motmethod为多目标跟踪method,即Multi-object Tracking,用于跟踪视频中的目标,并为目标分配track_id,目前在aiexpress中使用的跟踪策略主要是基于卡尔曼滤波和IOU作为算法基础。本文将对motmethod的算法和实现做相关介绍。
2.算法介绍
目前aiexpress的motmethod主要是基于卡尔曼滤波和IOU的跟踪算法,根据目标的位置信息进行跟踪。
算法主要分3个步骤
1) prediction 利用卡尔曼滤波器预测轨迹在当前帧的位置;
2) match 利用预测位置和观测位置得到匹配结果;
3) update 根据匹配结果对轨迹集合进行更新;
这里的1)和3)属于卡尔曼滤波的预测和修正的步骤,2)属于匹配算法范畴,本文后半部分主要介绍这两个部分。
2.1 卡尔曼滤波
2.1.1 任务
在我们的多目标跟踪系统中,需要根据track在n-1时刻的最佳估计状态来推测当前时刻n的估计状态(并非最佳),然后再和观测到的target匹配。那么卡尔曼滤波的任务主要是一下两个方面:
1)根据track在n-1时刻的最佳估计状态X(n-1|n-1)推算出n时刻的估计状态X(n|n-1),也称为先验估计;
2)融合n时刻的观测状态X(n)和先验估计X(n|n-1)得到更为准确的后验估计X(n|n),以此作为n+1时刻状态的预测基础。
2.1.2 原理
本章节主要介绍卡尔曼滤波两大任务的原理。
1) 任务1:预测
首先,卡尔曼滤波假设系统中目标的位置和速度都是随机的,且都服从高斯分布。每个状态变量有一个均值μ,以及方差 σ2。在高斯分布中,均值μ是随机分布的中心,也是最有可能的状态。
假设我们的目标跟踪系统里有两个状态量,分别是位置p和速度v,那么该系统的不确定性可由协方差P表示:

Pij表示第i个和第j个状态变量之间的相关性,在位置p和速度v不相关的系统,非对角线元素都为0。
下面我们基于高斯分布建立状态变量,在n-1时刻的状态变量为:

经过时间间隔t,n时刻的状态为

这里我们有一个假设,就是本系统没有控制量B(n),类似加减速的控制变量。
转换矩阵F为
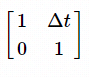
完成状态变量预测之后,我们也要对协方差矩阵应用转换函数,更新协方差矩阵。但是因为存在外部干扰,仅仅做转换是不够的。这里我们要对协方差P增加一个噪声的协方差矩阵Qn,那么对协方差P更新后为
从上式我们发现协方差P的值在增大,也就是说经过预测后状态变量的不确定性在增加,说明预测值和真实值相差越来越大,因此,我们需要通过卡尔曼滤波的修正步骤来提高估计值预测的准确性。
2)任务2:修正估计值
这一步骤是修正前面得到的先验估计,最小化其和真实值之间的差距。
在实际情况下,测量值X(n)并不能直接测得,需要通过实际测得的Z(n)经过变换H得到X(n),这里的Z(n)和X(n)因为不在一个空间尺度里,所以需要借助H将它们映射到同一空间。比如在测距仪系统,只能测得时间间隔,而非实际距离,此时需要借助矩阵H将时间测度转换到距离测量空间,这里的V是测量误差。

测量值的不确定性用协方差R(n)来表示,而在得到测量值Z(n)的情况下,其最有可能的高斯分布就是以Z(n)为均值的高斯分布。
我们可以对比一下在预测步骤中,我们是已知前一帧状态量的高斯分布,通过变换方程得到当前帧状态量的高斯分布,然后推断出其中可能性最大的预测值。
而在这里,我们是已知当前帧的测量值Z(n),然后估计出测量值的高斯分布,和预测步骤是一个逆过程,也是一个贝叶斯推断的过程。
目前我们得到两个高斯分布,分别是估计值X(n)和测量值Z(n),我们需要融合这两个结果,得到最佳估计。显然,这两个分布的相交部分是真实值最有可能的分布(注意要将X(n)和Z(n)映射到同一空间),那么将两个高斯分布相乘即可。于是,我们得到新的分布,其均值为X(n|n)也就是我们当前状态的后验估计,方差为P(n|n),这里的K称为卡尔曼增益:



上式我们看到,经过修正步骤后,P值减小,也就是X(n|n)的不确定性降低了,X(n|n)也就是后验估计。
另外,从K的计算方式(5)来看,K和先验估计的协方差P成正相关,和测量噪声协方差R成负相关。
当P越大时,K值越大,后验估计更接近于测量值Z(n);当R越大时,K值越小,后验估计更接近于先验估计,这也是我们在具体实现时指导调参的依据。
2.2 匹配算法
该部分主要用于匹配检测框target和已跟踪到的track,对匹配成功的检测框分配已跟踪目标的id,对未匹配上的目标分配新的id。这里用的匹配测度是IOU,也就是检测框和跟踪目标的交并比,其数学表达式如下:

IOU越大,表示A和B的匹配程度越高

这样我们就可以建立target和track的iou邻接矩阵aff,举例来说:
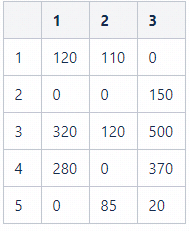
这里aff[1][2]表示track[1]和target[2]的IOU是110。
2.2.1 简单匹配
本节我们在邻接矩阵的基础上进行简单匹配。
简单匹配的原则是track要选择和它IOU最大的target,同时target也要选择和它IOU最大的track,如果两者相互选择了对方,那么简单匹配成功。在上面的矩阵中,track[3]和target[3]互为对方最大的IOU,那么我们给target[3]分配的id就是3。
2.2.2 匈牙利匹配
完成简单匹配后,当前邻接矩阵为:
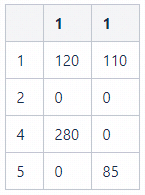
匈牙利匹配的核心思想是匹配之后使得整个系统的IOU最大,比如在我们当前的邻接矩阵中,将target[1]和track[4]匹配,target[2]和track[1]匹配,可以使整个系统的IOU最大,但是在一些情况下匈牙利匹配得到的匹配结果可能不是唯一的,AIExpress在IOU2实现中也只使用了简单匹配。
3. AIExpress实现
本章节主要介绍AIExpress如何实现mot算法,并介绍下相关配置的含义。
3.1 输入输出
输入
输出
3.2 卡尔曼滤波建模
我们在前面了解了卡尔曼滤波原理,本节主要介绍如何将卡尔曼滤波应用到我们的系统中。
首先我们确定系统的状态矩阵,这里我们目标box的状态变量为X(n)= [x, y, s, r, dx, dy, ds]
分别表示box的中心坐标(x,y),box的面积s,box的宽高比r,后面三个状态为前三个状态量相邻帧之间的差值。
测量值为Z(n) = [x, y, s, r],那么就有如下几个变换:

上式通过状态转移矩阵得到先验估计X(n|n-1)。
另外,测量值和状态值的转换过程如下:

通过以上步骤,我们完成了对检测框跟踪的卡尔曼滤波建模,这里还需要协方差矩阵P,测量协方差R和噪声协方差Q,这三个值可根据具体场景做相应调整。
AIExpress中卡尔曼滤波实现的核心代码如下:
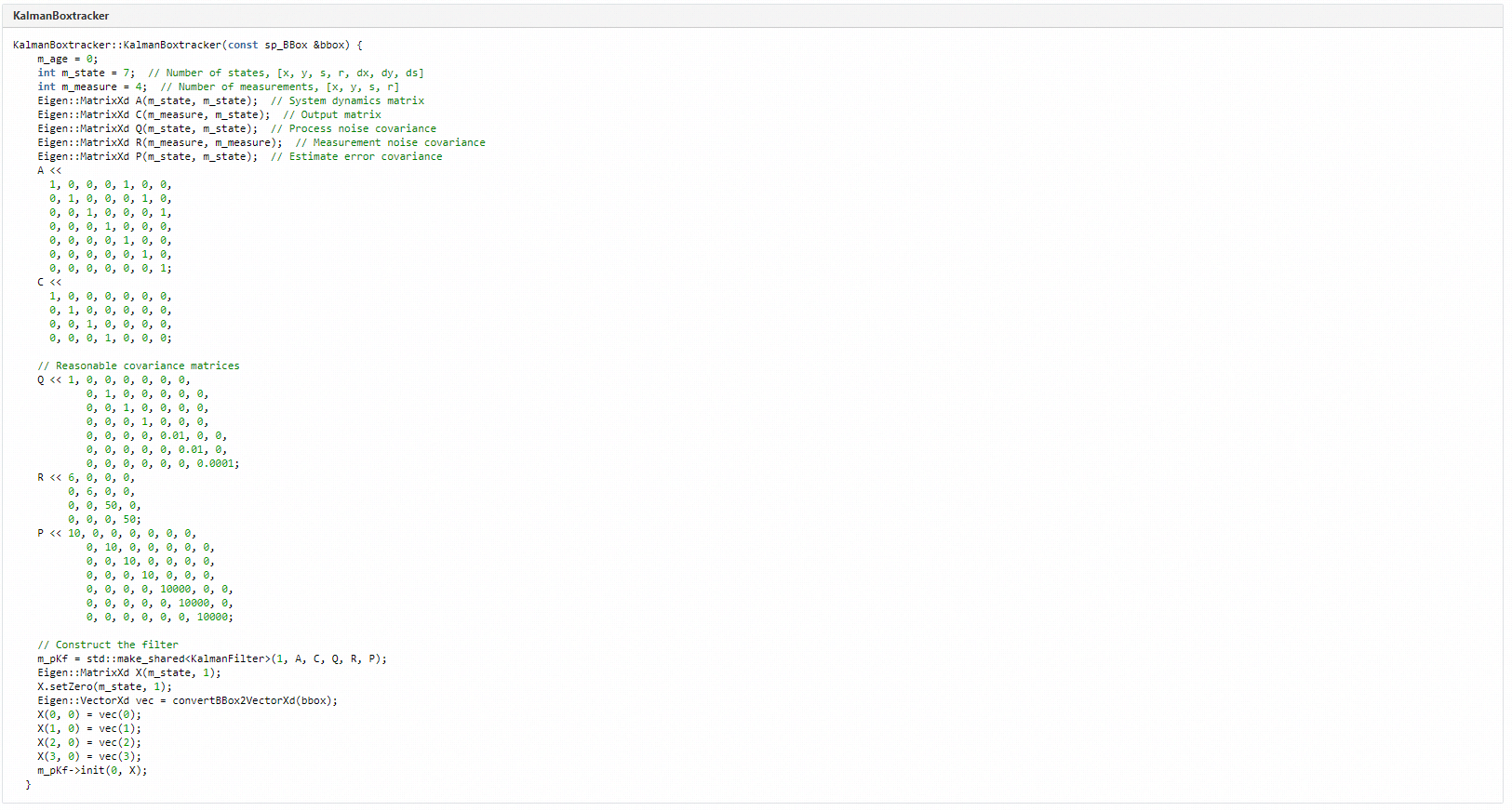
完成模型建立后,就可以按照按原理的预测和修正步骤,实现我们系统的卡尔曼滤波,具体实现如下:

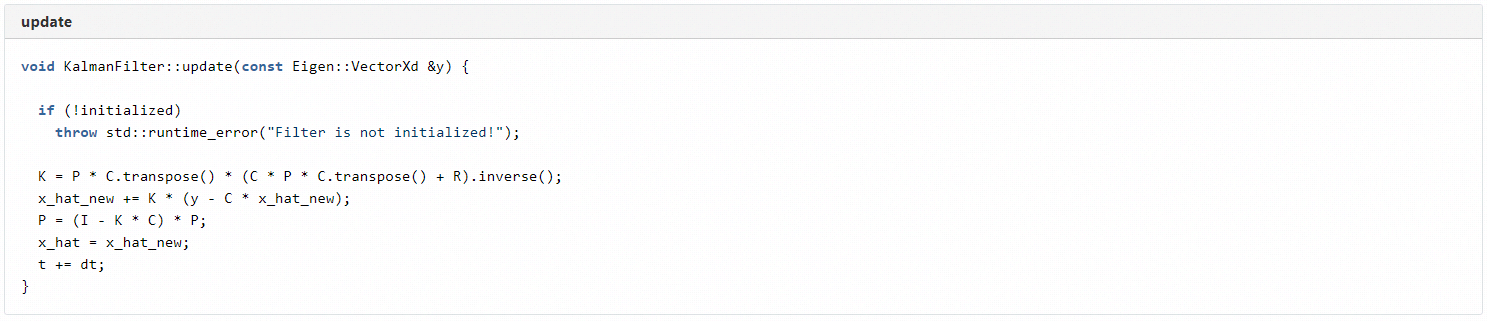
以上即完成了卡尔曼滤波在我们系统中的应用。
3.3 mot代码实现
3.3.1 重要数据结构
Target为目标检测框,body_box保存当前框的信息。
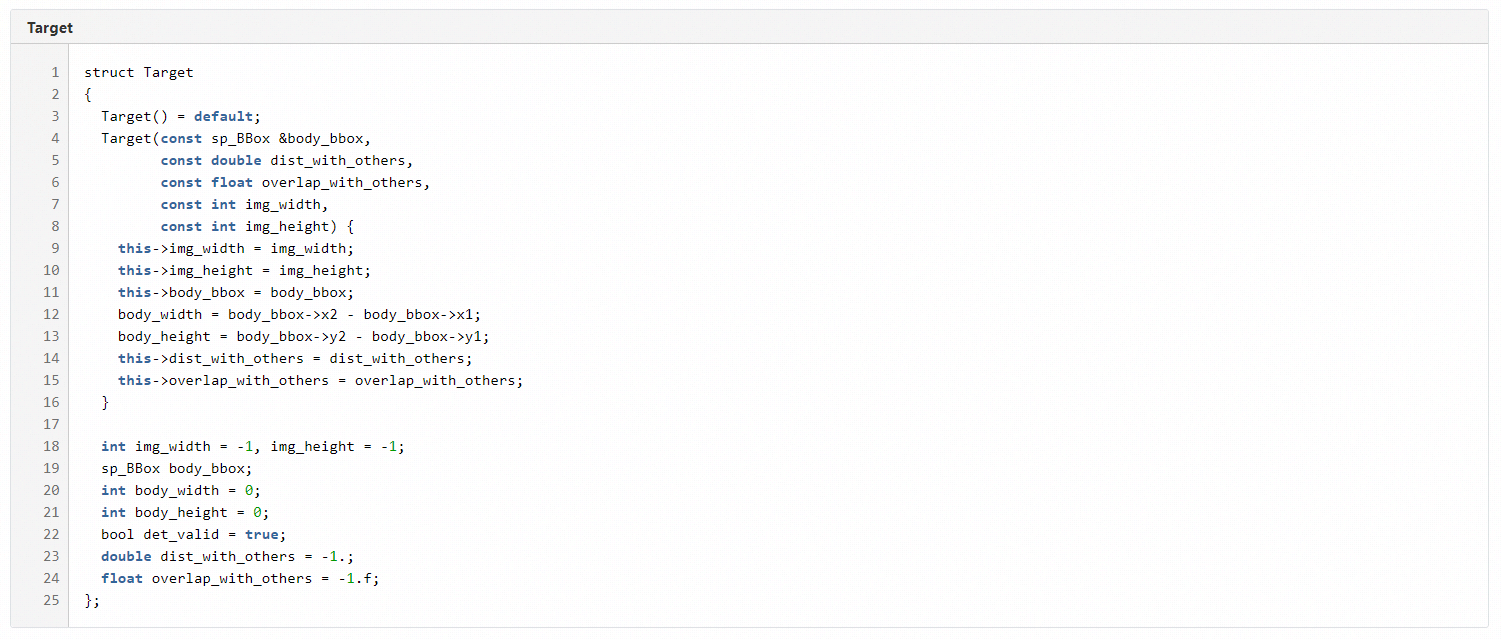
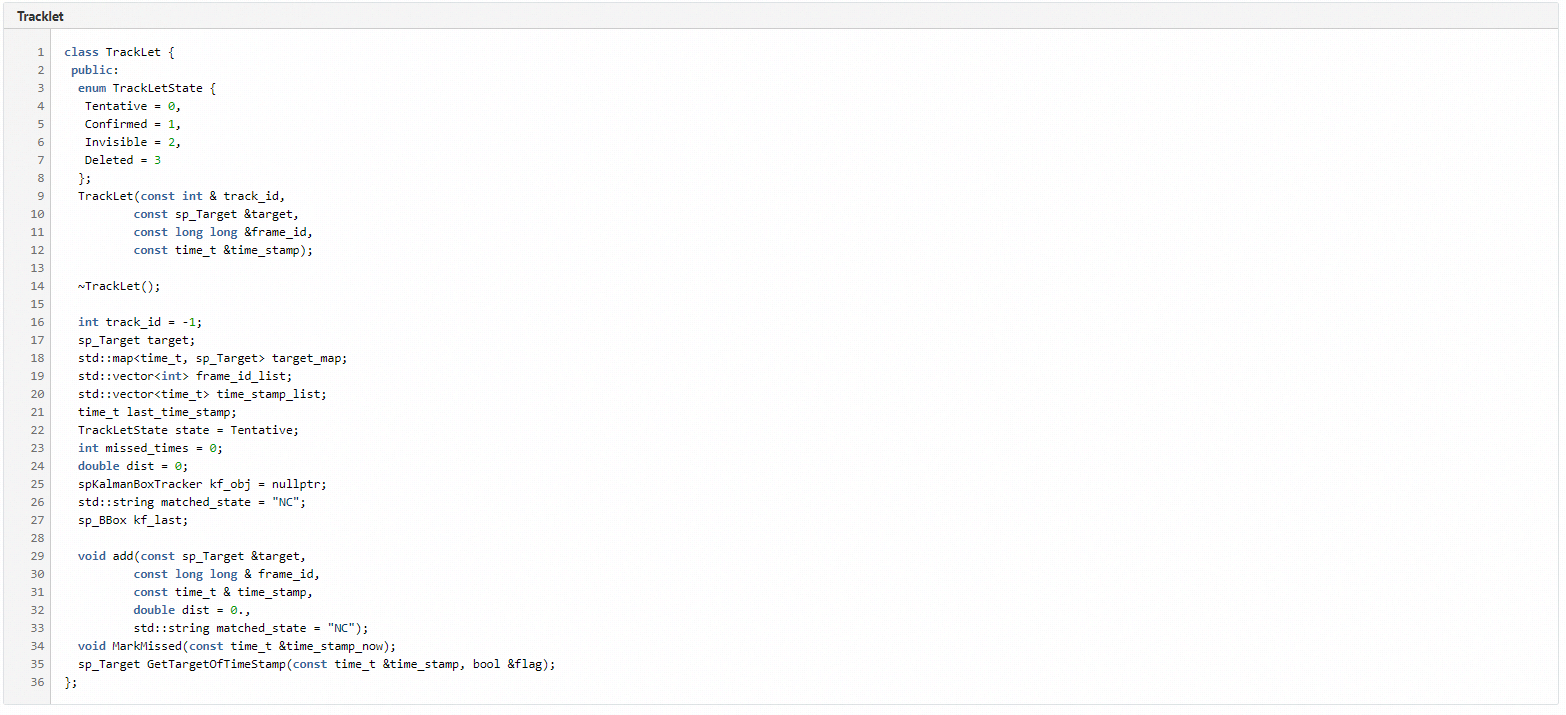
TrackLet为某一目标的轨迹片段,其中target_map表示target在一段时间序列下的信息。它维护了4种状态,其中Tentaive表示待分配id,Confirmed表示已确认,Invisible表示该目标在当前帧不可见,Deleted表示该目标已经消失,即disappeared_id。
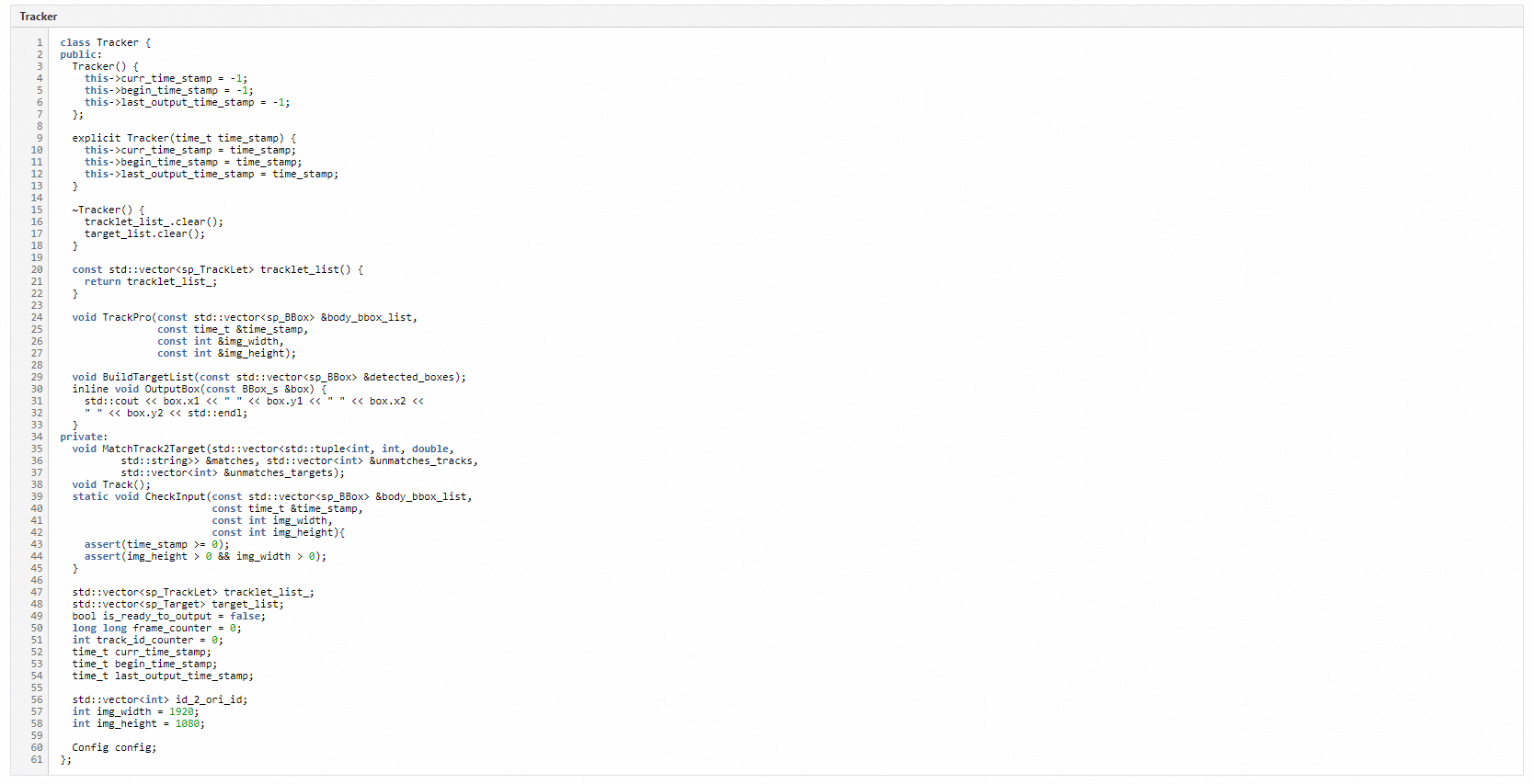
Tracker为实现目标跟踪的类,其中核心接口是TrackPro,该接口完成3个步骤。
1)利用卡尔曼滤波对已出现的tracklet进行位置预测;
2)筛选当前帧出现的检测框,不跟踪遮挡较为严重的目标框,这里的阈值都可在配置中修改;
3)匹配track和target,更新tracklet的轨迹。
3.4 配置管理
motmethod提供了算法相关参数的配置,本节对配置参数做详细说明,用户可根据具体场景修改参数适配。